What if there was a magic formula that could help you write blog posts faster than ever before? And what if this formula also made your content clearer, easier to follow and more engaging for your readers?
If only, right?
We don't have a magic formula for you, but wegot something just as good: content patterns.
In this post, you'll discover how to use content patterns to create blog posts in a structured way, beat writer's block and cut hours from your usual content creation process.
“There’s Always More to Write and Never Enough Time…”
Whether you're running the show solo, leading a team, or crafting those killer posts that draw people in, we all hit the same wall. Too much to say, too little time to say it.
We've all been there, feeling the crunch of deadlines and the pressure to perform. It's like being stuck in a cycle, knowing there has to be a better way but not quite sure how to break free.
That's exactly why we're here to show you a ridiculously easy way to shave hours off of your current content writing strategy.
This isn't just about working faster; it's about making your whole process smoother and more effective, so you can put out the required content to get Google’s attention and get the right eyes in front of your content.
It Starts With Your Blog Post Structure…
You don’t need to make drastic changes to your current posts – remember, we’re saving time to focus on quality here.
A universally useful structure for any piece of content you create looks like this:

The intro always explains what your post is about, whom it's for and why it's worth paying attention to. The intro explains how the reader will benefit from continuing to read.
The content pattern is where you explain your core ideas, list your products, provide your step-by-step recipe, or outline your strategies.
The call to action closes off your post. This is where you tell your readers what to do next, whether that's leaving a comment, checking out another related post, signing up to your newsletter, or anything else that's important to your business.
Even if you do nothing else, you'll already benefit greatly from creating a "scaffold" for each blog content design, with these three building blocks.
In today's post, we're mainly concerned with that middle section of the basic layout: the content pattern.
Now, What Is A Content Pattern and How Do They Help?
A content pattern is a layout that repeats several times throughout a post.
A typical example is a list post: every item in the list has an image, a heading, sometimes a sub-heading, and some text. For each item in the list, these same elements are repeated in the same order, using the same formatting. The structure of the content ends up looking like this:
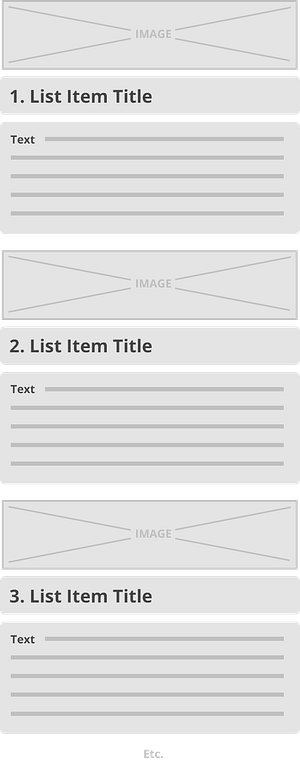
One of the advantages of this design pattern is that you only have to think about the formatting and layout once and then you simply repeat that pattern for every list item.
This content pattern makes up the majority of a blog post. Use it well and you can easily create beautifully formatted, content-rich posts that offers value and a memorable user experience.
What Are the Different Content Patterns?
CONTENT PATTERN 1:
What, Why, How

The headline is a summary of what this section of the pattern is about. This can be a product you're reviewing, a step in a multi-step process or recipe, a core idea you want to convey.
The first text section ('what') elaborates on what it is that you're describing in this section. Think: objective, factual description.
The second text section ('why') describes why it matters. Why are you mentioning this core idea? Why is this step in the process important?
The third text section ('how') describes how to make use of this new information. How to put this core idea into action. How to perform this step in the process or recipe.
Practical Use Cases for this Content Pattern:
- Educational Content & Tutorials: Explaining LinkedIn marketing? Start with a simple definition (what), highlight its potential to improve a business’s sales (why), then guide your reader through steps to implement (how).
- Product Reviews: Covering a new smartphone? Describe its standout features (what), discuss how it sets new standards for performance or photography (why), and suggest ways to maximize its use (how).
- Recipes & DIY Projects: Sharing a cake recipe? Introduce the type of cake and what makes it special (what), explain the joy of baking from scratch or the cake's unique flavor profile (why), then walk through the recipe steps (how).
- Health & Fitness Guides: Introducing a yoga routine? Describe the sequence of poses (what), delve into the benefits for mind and body (why), and provide a detailed routine for beginners to follow (how).
Example: Blog Post About Healthy Habits
Here's what one loop of the "what, why, how" content pattern could look like on a health blog:

CONTENT PATTERN 2:
Person, Problem, Solution

The first part describes a person or a story. It sets the scene and helps readers relate.
The second part describes a problem this person has. An obstacle they face, a challenge they must overcome.
The third part describes the solution our protagonist put into place.
You can think of this as a storytelling format for providing actionable information with a personal touch. You'll find this type of pattern applied in almost every bestselling non-fiction book.
Practical Use Cases for this Content Pattern:
- Case Studies: [Person: "Alex," a small business owner struggling with online visibility.] [Problem: The challenge of attracting online traffic and converting it into sales.] [Solution: Implementing a customized digital marketing strategy that effectively doubled their online sales.]
- Self-Help: [Person: "Jordan," constantly overwhelmed by procrastination and unable to meet deadlines.] [Problem: The ongoing battle to manage time effectively and complete tasks.] [Solution: The discovery and adoption of a transformative time-management technique, leading to improved productivity and a better work-life balance.]
- How-To Guides: [Person: "Sam," a beginner wanting to create a website but unsure of how to begin.] [Problem: Feeling lost among the vast options for platforms and bogged down by technical jargon.] [Solution: Following a clear, step-by-step tutorial that demystified the process, leading to the successful launch of their first website.]
- Marketing Wins: [Person: "Casey," struggling to make a mark with their brand on social media.] [Problem: The difficulty of engaging an audience and standing out in a saturated online space.] [Solution: Employing a unique content strategy that resonated with their target audience, leading to viral success and brand growth.]
Example: Ways to Eliminate Stress for Every Personality Type
Here's what this content pattern could look like on a lifestyle blog:

CONTENT PATTERN 3:
Pros, Cons, Action

The first part is about the pros. The good stuff. What you like about a product, what a case study object does well.
The second part is about the cons. What you don't like about the product. Where the case study object has room for improvement.
The third part is a summary of what we can learn from these pros and cons. What action we should take next. How we can decide whether or not to use this product.
Practical Use Cases for this Content Pattern:
- Product Reviews and Comparisons: Ideal for giving readers a balanced view of gadgets, software, books, or any product. By discussing what works (Pros) and what doesn’t (Cons), you help readers make an informed decision, concluding with a recommendation (Action).
- Lifestyle Changes and Wellness Programs: For posts on diets, fitness routines, or wellness apps, highlight what users have found beneficial (Pros), point out where they might fall short (Cons), and provide a verdict on their overall effectiveness (Action).
- Technology and App Reviews: Dive into the latest technology or apps by detailing their innovative features (Pros), critiquing usability or functionality issues (Cons), and concluding with who would most benefit from them (Action).
Example: Which Flagship Smartphone is Right for You?
This content pattern is very well suited for product reviews and list posts. Here's an example of how it could be used on a tech blog:

CONTENT PATTERN 4:
Facts, Opinion

This is a pattern that's very well suited for curated content or any kind of content where you pull in various facts and stats to make your point. The pattern is simple: in the first part, introduce the facts. In the second part, provide your personal opinion. The second part is also where you can provide context and write about what the facts mean, combined with all the other facts you list in your post.
Example: Scientifically Proven Study Hacks
Here's an example of how this pattern could be used in a blog post about effective learning:

Turn Your Content Patterns into a Ready-Made Formula
Content patterns are your surefire solution to kissing writer’s block and blank page dread goodbye.
Instead of looking at your screen wondering where (or how) you’re going to write out the next post, you have a focused approach to use instead.
First, find Your Patterns
What type of content do you write the most? How-to guides? Product reviews? Assign a specific content pattern to each blog post type, and create outline templates for each one.
For example:
If you share success stories regularly, use Content Pattern #2: Person, Problem, Solution as your writing template.
Your blog post structure would look like this:
Intro
Content Pattern
Person: Customer Name
Problem: Challenges they had before encountering your product or service
Solution: Their life now with after buying and using your product
Conclusion
Now you have a template to fill your content where it should go, saving you hours in deliberating and doubting yourself.
Do the same for any other blog post types you have, create outline templates in Google Docs, or any other writing tool. You’ll find it much easier to fill out your posts and increase your content output!
But there’s one more step…the actual blog post design. What if you could set up your content patterns, on your website, in less than a minute?
Well, with Thrive Architect’s content blocks, you can.
Wait, What’s Thrive Architect?
Thrive Architect is the tool you need to create high-quality, engaging blog posts fast.
With this tool, you can directly translate your content patterns into visually appealing blog content.
Whether it's the "Person, Problem, Solution" structure or a step-by-step "How-To" guide, Thrive Architect allows you to drag and drop pre-designed content blocks that align with your templates — for any blog content type.
This means you can replicate the structure of your Google Docs outlines on your website, maintaining the flow and integrity of your content, without touching a line of code. No HTML. No CSS.
Think of it as premium UX design at your fingertips — without you needing to do any of the work.

Examples of Thrive Architect Block Templates
The beauty of Thrive Architect lies in its flexibility. Every content block can be tailored to match your brand's aesthetic, voice, and overall web design. From changing font sizes to adjusting color schemes, Thrive Architect gives you the control to make each post uniquely yours while keeping the consistency that your audience appreciates.
So if you want your blog posts to share the same color scheme as your homepage, for example, you can easily make this happen in one click.
Beyond individual blocks, you can use this tool to save entire blog layouts as templates. Imagine finishing a blog post and knowing that you can reuse the same successful format with a few clicks next time. Talk about streamlining your content creation workflow.

This feature is a game-changer, especially for series or recurring post themes, allowing you to maintain a consistent look and feel across your site while dramatically cutting down on setup time.
Thrive Architect doesn't stop at just making your posts look good; it equips you with tools to make them more interactive and engaging. From customizable call-to-action buttons, to dropdown menus for better navigation, and testimonial blocks that bring customer stories to life, Thrive Architect will help keep your readers stay hooked from start to finish.
Next Steps: Optimize the Quality of Your Writing
Since we’re talking about creating better content, let’s not forget the heart of the matter: quality really matters.
What you write is just as important as your visual design system.
Keep it real with your unique voice, double-check your facts, give your work a good edit to make it shine, and listen to what others have to say. Keeping it simple and genuine like this can turn your new content from being just okay to totally standout.
Here are a few tutorials to help you draft effective content consistently:
Ready to Create Better Content, Faster?
Initially, it will take some effort to think about content design patterns and figure out how to use them in your posts. It may even feel a bit uncomfortable, at first.
But stick with it. The payoff comes once you get accustomed to the basics of using these patterns.
Think of them as your personal style guide, constantly showing you how to frame your content from a written and design perspective.
The more you get used to content patterns, the more ways of using them open up. They become a way to add structure and flow even to the most complex topics and the most epic posts. Totally changing your content management system and helping you hit those publishing goals on the daily.






